LẠM PHÁT VŨ TRỤ
LẠM PHÁT VŨ TRỤ
44B
Lịch sử tóm tắt của vũ trụ
Hình 1. Lịch sử tóm tắt của vũ trụ: các thời kỳ và thời điểm tương ứng
Vũ trụ đã trải qua những thời kỳ sau (xem minh hoạ ở hình 1)
1 / Thời kỳ Hấp dẫn lượng tử (kéo dài đến thời điểm 10^-43 giây),
2 / Thời kỳ Thống nhất lớn (kéo dài đến thời điểm 10^-34 giây),
3 / Thời kỳ Vũ trụ lạm phát, trong thời kỳ này phát sinh các nhiễu loạn và
SHD (sóng hấp dẫn).Tiếp theo là thời kỳ điện yếu (kéo dài đến thời điểm
10^-10 giây),
4 / Thời kỳ ngự trị của Bức xạ (Radiation dominated era) (kéo dài đến thời
điểm 10^2 giây),
5 / Sau đó là thời kỳ ngự trị của vật chất (Matter dominated era)(kéo dài đến
thời điểm 10^13 giây). Trong thời kỳ này hình thành các nguyên tử, bức
xạ và vật chất tách rời nhau, CMB (Cosmic Microwave Background-Bức
xạ phông) xuất hiện,
6 / Sau thời kỳ này vũ trụ chuyển sang trạng thái trong (transparent) đối với
photon,
7 / Thời kỳ hình thành các sao và thiên hà,
8 / Thời kỳ hiện tại.
Những nhiễu loạn gây nên bởi lạm phát
Thời kỳ lạm phát (thời kỳ 3 trên hình vẽ 1) gây ra 2 loại nhiễu loạn quan trọng: vô hướng (mật độ) và tensor (SHD). Nhiễu loạn vector mau chóng phân rã.
Nhiễu loạn vô hướng được cảm ứng bởi các bất đồng nhất năng lượng mật độ . Những nhiễu loạn này quan trọng vì đó sẽ là mầm của các cấu trúc vũ trụ trong tương lai.
Những nhiễu loạn tensor ứng với SHD.
Hai nhiễu loạn vô hướng và tensor có thể được xác định bởi sự tiến triển của một hàm vô hướng F gọi là inflaton thoả mãn điều kiện gọi là “lăn chậm” (slow roll).
Như chúng ta biết phương trình Einstein có 2 vế, vế trái chứa metric gmn (m,n là chỉ số tọa độ) mô tả hình học của không thời gian còn vế phải chứa tensor năng xung lượng Tmn (m,n là chỉ số tensor)
mô tả vật chất. Các nhiễu loạn của metric xuất hiện dưới dạng các vô hướng thường được ký hiệu là A, B, E, F, và tensor được ghi là Dij(i,j là chỉ số tensor) ,xin xem tài liệu đặc biệt quan trọng [1].
Bên vế phải tensor Tmn được biểu diễn theo mô hình chất lỏng lý tưởng và chứa p=áp suất,r=mật độ và um(m là chỉ số vector)= vector vận tốc 4-chiều.Chúng ta cũng cần lấy nhiễu loạn của Tmn như đã làm đối với nhiễu loạn vô hướng. Trong trường hợp nếu vật chất là một trường F (inflaton, Higgs,…) với thế năng V(F) thì các đại lượng p,r và um được biểu diễn qua F và V(F) (um tỷ lệ với đạo hàm riêng theo tọa độ m của F).
Nhiễu loạn vô hướng
Ta phải chọn một đại lượng vô hướng Z bất biến chuẩn. Điều đó có nghĩa chọn một vô hướng thế nào cho đại lượng đó bất biến đối với biến đổi toạ độ. Điều này dẫn đến Z=A / 2, đại lượng này được gọi là nhiễu loạn độ cong (gắn liền với mật độ).
Lạm phát vũ trụ
Lạm phát (inflation) là hiện tượng vũ trụ dãn nở cực nhanh trong một thời đoạn vào buổi sơ sinh của vũ trụ.Giai đoạn sơ sinh của vũ trụ quan trọng nhất là những thăng giáng lượng tử trong thời kỳ lạm phát.Trong lạm phát những thăng giáng lượng tử vi mô sẽ tỏa rộng lên kích thước vĩ mô tạo nên mầm cho những cấu trúc kích thước lớn như các thiên hà
Hiện chưa có một lý thuyết hoàn chỉnh về lạm phát song dường như các nhà vật lý thiên về giả thuyết ngưng tụ của một trường vô hướng của hạt inflaton.
Ngày 17 tháng 3/2014 các nhà vật lý của thí nghiệm BICEP2 ( Background Imaging of Cosmic Extragalactic Polarization (California Institute of Technology) ở Nam Cực đã thông báo tìm ra dấu vết đầu tiên của lạm phát vũ trụ (Cosmic inflation) và sóng hấp dẫn (Gravitational wave).
Song những dữ liệu do vệ tinh Planck (dự án của ESA-European Space Agency) cung cấp đã gây nên nghi vấn liệu tín hiệu ghi đo bởi Bicep2 có thật sự thuộc về CMB (Cosmic Microwave Background) hay đó là thuộc bụi thiên hà nằm trên phông ( Galactic Dust Foreground) tức là thuộc về những giai đoạn sau này trong lịch sử vũ trụ. Rất có thể bụi thiên hà đã tạo nên tất cả hoặc phần lớn tín hiệu phân cực của Bicep2.
Các tác giả của lý thuyết lạm phát có thể kể đến là: Alan Guth (MIT), Andrei Linde (Stanford) và Starobinsky, Steinhardt, Albrecht, Sato,...
Để minh họa vấn đề ta xét mô hình một trường (single field).Ta xuất phát từ hàm tác động ( action):
(ý nói hàm V nhiều lần lớn hơn sự biến thiên của hàm ) thì hàm V có một đoạn phẳng kéo dài và trong đoạn này xảy ra lạm phát . Như vậy phải có đoạn SR để kéo dài quá trình lạm phát. Đến một thời điểm nào đó của F thì V biến thiên đột ngột làm cho lạm phát kết thúc gây nên một chuyển pha bậc 1 (trong quá trình chuyển pha này không loại trừ sự phát sinh sóng hấp dẫn). Tiếp theo đó là quá trình tái nóng dần (không còn lạm phát gây nên sự làm lạnh không gian ).
Có nhiều mô hình về inflation . Sau đây chúng ta giải thích thế nào là SR trên một ví dụ đơn giản.
Ta lấy một ví dụ về trường vô hướng.
Hình 2 . Biến thiên của hàm V
Theo phương trình trên sự dãn nở vũ trụ tương đương với giai đoạn
r+3p < 0, song vì mật độ r là dương cho nên áp suất p phải là âm, điều này có nghĩa là ta đang có giai đoạn hấp dẫn đẩy gây dãn nở vũ trụ. Đấy là nguyên nhân của lạm phát.
Thống kê không Gauss(non-gaussianities)
Ở phần trên ta đã nói đến các hàm liên kết (correlation function) hai điểm,đó là các phổ công suất PZ (Z là chỉ số).
Song các phổ gắn liền với hai điểm chỉ cho ta những thông tin về phân bố gọi là phân bố Gauss.Những thông tin về phân bố Gauss không cho phép chúng ta tìm hiểu được những mô hình lạm phát một cách tường tận.
Các tính toán của các nhà vật lý chứng tỏ rằng các thiên hà và các cấu trúc khác dường như không phân bố từng đôi một (ứng với Gauss) mà thay vì có khuynh hướng sắp xếp thành những cấu hình phức tạp hơn: tam giác ,chữ nhật, ngũ giác , … và các hình dạng khác (ứng với non-Gaussianities).
Các trường inflaton, hấp dẫn và mọi trường khác khả dĩ hiện hữu lúc sơ sinh của vũ trụ : các hạt trong các trường này biến đổi qua nhau và tán xạ lẫn nhau tạo nên những tam giác và các hình khác .
Hình3.Theo lý thuyết lạm phát lúc vũ trụ sơ sinh xuất hiện nhiều cặp hạt, một số cặp hạt phân rã thành 3 hạt inflaton tạo nên cấu hình tam giác (ứng với bispectrum).
Các tam giác sẽ dẫn đến 3 điểm nóng trên CMB và tiếp theo cụm 3 thiên hà . Các tam giác đó và các hình khác tạo nên những type hình dạng trong giai đoạn lạm phát.
Vì vậy cho nên chúng ta cần tính toán hàm correlation của ba điểm BZ (phổ đôi-bispectrum), của bốn điểm TZ (phổ ba-trispectrum),… Sau đây chúng ta hạn chế đến phổ đôi. Song về nguyên tắc ta có thể nghiên cứu các phổ bậc cao hơn ứng với nhiều hình dạng phức tạp hơn hình tam giác.
vậy các vector xung lượng làm thành hình tam giác và phổ đôi (bispectrum) chỉ phụ thuộc vào độ lớn của các xung lượng mà không phụ thuộc vào chiều của các xung lượng.
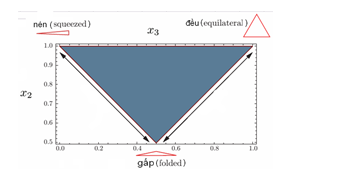
Như vậy hàm phổ đôi là một hàm của các xung lượng với nhiều cấu hình tam giác khác nhau của các xung lượng đó.Trên hình 4 ta thấy có ba cấu hình cực trị: nén-squeezed, gấp-folded và đều-equilateral.
Trên thực nghiệm người ta cần xác định hình dáng các cấu hình này để so sánh với lý thuyết.
Hình 4 .Cấu hình xung lượng của phổ đôi ( bispectrum)
3/ Mô hình curvaton (Curvaton model)
Ngoài trường inflaton có một trường vô hường light( light có nghĩa là khối lượng nhẹ ) cũng thu được các thăng giáng lượng tử . Nếu mật độ năng lượng của trường vô hướng này nhỏ trong quá trình lạm phát thì các thăng giáng đó là gọi là thăng giáng isocurvature.Trường vô hướng có được các thăng giáng này gọi là trường curvaton.
Tính toán theo các mô hình
Kết quả thực nghiệm so sánh với lý thuyết
Một số dữ liệu thực nghiệm [8]
KẾT LUẬN
Bài viết này chỉ nêu được một số mô hình lạm phát và cũng chỉ giới hạn đến các hàm correlation 3 điểm (tam giác).
Hiện nay thì các nhà vật lý thực nghiệm đang truy tìm trên bầu trời vũ trụ những cấu hình như tam giác (ứng với các hàm correlation 3 điểm) và các hình dạng phức tạp hơn (ứng với các hàm correlation nhiều điểm hơn) để thu dữ liệu cơ sở nhằm xây dựng hoàn thiện giả thuyết lạm phát , một giả thuyết quan trọng để hiểu các giai đoạn sơ sinh của vũ trụ. Cũng cần nhấn mạnh rằng giả thuyết lạm phát có khả năng nối liền vũ trụ học (cosmology) với lý thuyết các trường lượng tử (Quantum field theory ).
Tài liệu tham khảo
[1] StevenWeinberg, Cosmology,Oxford
[2] Juan Maldacena,Non-gaussian features of primordial fluctuations in
single field inflationary models
https://www.google.com.vn/webhp?sourceid=chrome-instant&ion=1&espv=2&ie=UTF-8#q=Non-gaussian+features+of+primo+rdial+%C2%B0uctuations+in+single+%C2%AFeld+in%C2%B0ationa+ry+models+Juan+Maldacena
[3] Sasaki ,Standard slow roll inflation
https://www.apctp.org/conferences/2010/awspc5/file/sasaki2.pdf
[4] Pascal Vaudrevange, Slow roll inflation
http://www.desy.de/~westphal/workshop_seminar_fall_2010/slow_roll_inflation.pdf
[5] Natalie Wolchover,Physicists Hunt for the Big Bang’s Triangles
https://www.quantamagazine.org/20160419-string-inflation-triangles/
[6] Daniel Baumann,The Physics of Inflation A Course for Graduate Students in Particle Physics and Cosmology
[7]E. Komatsu et al.,Non-Gaussianity as a Probe of the Physics of the Primordial
Universe and the Astrophysics of the Low Redshift Universe
[8] Tomo Takahashi,Primordial non-Gaussianity and the inflationary Universe
Prog. Theor. Exp. Phys.2014, 06B105 (31 pages)
DOI: 10.1093/ptep/ptu060
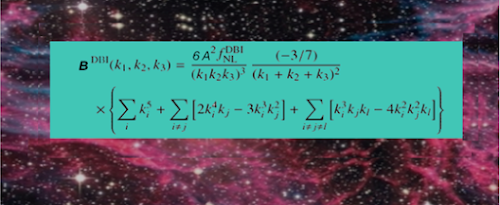















Nhận xét
Đăng nhận xét