VẬT CHẤT SỐNG VÀ KHÔNG SỐNG (LIVING AND NON LIVING)
Thông tin tổng quan chung quanh vấn
đề vật chất sống và không sống
ABSTRACT
Is it possible to reconcile our
concepts on the living kingdom and the non-living kingdom?
Many centuries separate these two
kingdoms. The adherents of vitalism believe that it exists a vital
force that organizes all living
organisms and dictates their behavior.
Presently physicists & chemists
seem to deny the vitalism philosophy and propose an approach for a preliminary
understanding of the self-organization observed in the living kingdom based on
the dissipative structure discovered by
Prigogine (Nobel prize 1977) and on the
complexity emergence developed by Laughlin (Nobel prize1998) and others. The
role of quantum theory in biology is
emphazised by physicists ( Schrodinger, Penrose,...) and a surprised analogy between Darwin doctrine and cosmology is pointed out by string
theoretician Leonard Susskind .
In addition the holographic universe
constructed by Bohm and Pribram indicates that there is an interconnectedness
between the living and non living kingdoms.
TÓM TẮT
Liệu có thể dung hòa các nhận thức
của chúng ta đối với hai vương quốc vật
chất sống và không sống? Nhiều thế kỷ đã phân chia hai vương quốc này. Các nhà
khoa học
theo thuyết sức sống tin rằng tồn
tại một lực sống đã tổ chức nên các cơ
thể sống và điều hành mọi hành xử của chúng.
Hiện nay các nhà vật lý và hóa học
dường như không tin vào thuyết sức sống
và đưa ra cách tiếp cận để tìm hiểu sơ bộ
quá trình tự tổ chức quan sát được trong vương quốc của sự sống dựa
trên những cấu trúc phát tán phát hiện
bởi Prigogine (Nobel 1977) và trên hiện
tượng đột sinh trong lý thuyết phức hợp phát triển bởi Laughlin (Nobel 1998) và
nhiều người khác. Các nhà vật lý (Schrodinger, Penrose,...) đã nhấn mạnh vai
trò của lý thuyết lượng tử trong sinh học đặc biệt mối tương đồng bất ngờ giữa
học thuyết Darwin và vũ trụ học đượclàm sáng tỏ bởi nhà lý thuyết dây Leonard
Susskind.
Thêm vào đấy vũ trụ toàn ảnh xây dựng bởi Bohm và Pribram
lại cho thấy rằng có mối liên thông giữa hai vương quốc vật chất sống và không
sống.
*
1
. Nhập đề
Năm 2009 chúng ta kỷ niệm 400 năm
Galileo Galilei sử dụng kính viễn vọng để quan sát bầu
trời và 150 năm Charles Darwin công bố
công trình có tầm quan trọng lớn đối với ngành sinh học On the Origin of Species , 1859 - Về nguồn gốc các loài. Hai sự
kiện lớn trên liên quan đến hai vương
quốc vật chất không sống và sống.
Sự phát sinh ở
thế kỷ XIX hai khoa học lớn là nhiệt
động học và thuyết DARWIN trong một thời gian lớn tưởng chừng như tách rời lẫn nhau thậm chí mâu thuẫn nhau.
Một bên, theo định luật 2 nhiệt động học thì các cấu trúc sẽ dần bị phá vỡ còn
thuyết tiến hóa Darwin thì chủ trương trong thế giói của vật chất sống có hiện
tượng vật chất tự tổ chức (self- organisation) dẫn đên những hệ có trật tự và có khả năng tái sinh.
Song giờ đây
với các thành tựu của nhiệt động học xa cân bằng người ta có thể chứng
minh đối với các hệ mở xa cân bằng có thể phát sinh những quá trình tự
tổ chức với cấu trúc có trật tự và có
khả năng tái sinh theo những thông tin được mã hóa trong hệ.
Nhiều người đã
cho rằng thế giới sống (living) và thế giới không sống (nonliving) là hai vương
quốc không dung hòa với nhau được, không thể nào ứng dụng các định luật nhiệt
động học vào thế giới sống. Thuyết sức sống (vitalism) cho rằng trong thế giới
sống có những lực sống đặc thù điều khiển các quá trình sinh học.
Hiện nay nhiều
nhà khoa học không nghĩ như thế, mặc dầu còn xa lắm mới có thể hiểu được bí mật
lớn của sự sống, song đã có nhiều công
trình nghiên cứu cho ta hiểu được ít nhất sự phát sinh nhiều cấu trúc trong thế
giới khách quan sau khi phát hiện các cấu
trúc phát tán (dissipative structure).
Một thời điểm
quan trọng là sự xâm nhập của cybernetics (điều khiển học) và synergetics.
Theo định nghĩa của Norbert Wiener điều khiển học [1a] là môn học về
điều khiển và trao đổi thông tin (communication) trong các máy móc và các sinh
vật , các tổ chức bao gồm cả các thực thể tự tổ chức
(self-organization). Louis Couffignal, một trong những người sáng tạo
cybernetics , xem cybernetics là nghệ thuật bảo đảm tính hữu hiệu của hành
động. Môn synergetics (tiếng Hy lạp có nghĩa là cùng hoạt động-working
together) sáng lập bởi Hermann Haken [1b], là môn học liên ngành nhằm giải
thích sự hình thành của các quá trình tự tổ chức trong các hệ mở nằm xa
cân bằng nhiệt động. Synergetics liên quan đến lý thuyết phức hợp, lý thuyết
các hệ động học, lý thuyết rẽ nhánh ( bifurcation), lý thuyết hỗn độn (chaos),
lý thuyết tai biến ( catastrophe theory).
Nhiều vấn đề
trong sinh học được nghiên cứu trên cơ sở của
lý thuyết động học vi mô (kinetics) vật lý : như sự hình
thành tự phát các cấu trúc từ các hệ phân tử mà không rơi vào mâu thuẫn với
định luật nhiệt động thứ hai . Động học vi mô (kinetics) được
định nghĩa là lý thuyết vi mô các quá trình xảy ra trong các hệ gồm nhiều phân
tử , nguyên tử nằm ở trạng thái không cân bằng.
Nhiều công
trình theo các hướng kể trên có thể dẫn đến những kết quả định lượng
(quantitative) đối với một số trường hợp hoặc kết quả định tính (qualitative) như khi ta sử dụng những lý
thuyết như lý thuyết tai biến ( catastrophe theory) vào phôi thai học .
Sự quan trọng
của thuyết lượng tử đối với sinh
học và mối tương đồng giữa vũ trụ học và
sinh học cũng được nhiều nhà vật lý nhấn mạnh và làm sáng tỏ (Schrodinger,
Penrose, Susskind, ...).
Cuối cùng lý
thuyết Vũ trụ toàn ảnh của
David Bohm & Karl Pribram lại cho
chúng ta thấy một quan điểm kỳ
diệu về sự kết nối liên thông (interconnectedness) giữa hai thế giới sống và không
sống minh chứng cho tính duy nhất của
hai vương quốc đó.
2 . Nhiệt động học, Cơ học thống kê và Lý thuyết động học vi mô (kinetics theory)
Trươc hết phải
nói rằng định luật II nhiệt động học chỉ áp dụng được với những hệ kín. Những
công trình của Schrodinger ( What is life ? 1944),Turing, Prigogine ,
Glansdorff,... đã mở đường cho sinh học phân tử . Trong những hệ mở (open) có
khả năng thu nhận entropy âm và vật chất từ môi trường bên ngoài
, có thể tồn tại những trạng thái dừng (stationary) ở
xa trạng thái cân bằng (far of equilibrium) với độ trật tự cao. Khi ở xa cân
bằng, hệ
được mô tả bởi những phương trình
phi tuyến (non linear) với những lời giải dừng (stationary). Nghiên cứu tính ổn
định của những lời giải này chúng ta sẽ có những trạng thái vật lý ổn định đối
với các thăng giáng nhiễu loạn . Còn các lời giải không ổn định lại sẽ dẫn hệ
đến những trạng thái ổn định khác và trạng thái cuối cùng sẽ có độ trật tự cao
hơn ứng với một đối xứng thấp hơn. Sự chuyển biến đến trạng thái ổn định
dừng được gọi là quá trình tiến hóa (evolution) và tuân theo nguyên lý Prigogine-Glansdorff. Quá trình này dẫn đến một hệ quả quan
trọng là khả năng
tự tổ chức (self-organisation).
Quá trình tự tổ chức
đòi hỏi sự có mặt của một hệ vĩ mô, gồm nhiều hệ con tương tác phi tuyến với nhau và phụ thuộc vào một số
thông số điều khiển. Trong quá trình tự tổ chức xuất hiện những tâm hút
(attractors) và tính phức hợp của tổ chức nội tại của một hệ mở tăng lên mà không cần đến một nguồn ngoại lai
nào. Sau đây là
các yếu tố quan trọng nhất trong việc tìm hiểu quá trình hình thành cấu trúc
[2a]:
1
. Có thông lượng entropy âm
2
. Hệ ở xa trạng thái cân bằng
3
. Các phương trình mô tả hệ là
phi tuyến
4
. Nguyên lý Prigogine-Glansdorff .
Nhờ những yếu tố trên mà trong những năm gần đây các nhà vật
lý, hóa học và sinh học đã tiến xa trong việc tìm hiểu sự hình thành các cấu
trúc trong những hệ mở. Song phải nói rằng
ta cũng còn xa mới hiểu hết các dạng phức tạp của thế giới sống quanh
chúng ta.
Nhiều bài toán về cấu trúc chúng ta
cũng gặp phải trong hóa học, khí tượng học, địa chất, vũ trụ.
Có thể nói bài toán về sự hình thành
các cấu trúc là một trong những bài toán cơ bản nhất của khoa học và nhận biết
được sự phát sinh các cấu trúc là một trong những vấn đề trọng điểm của nhận
thức luận.
Khái niệm về cấu trúc
Đối với toán học hiện đại khái niệm
cấu trúc là khái niệm quan trọng (Bourbaki- Cơ sở toán học). Khái niệm cấu trúc
liên quan đến khái niệm tập hợp, yếu tố tập hợp, liên hệ tương quan và các toán
tử. Vậy cấu trúc là sự tổ chức giữa các yếu tố và tính chất quan hệ giữa các
yếu tố của hệ. Khi nói đến cấu trúc chúng ta không quan tâm đến bản chất của
các yếu tố đó mà chỉ quan tâm đến mối liên hệ giữa chúng với nhau.
Trong các hệ vật lý người ta nói đến
các cấu trúc không gian và thời gian. Về cấu trúc không gian
người ta có thể sử dụng lý thuyết đối xứng (như trong tinh thể học
-cristallography). Về cấu trúc thời gian người ta sử dụng động học của hệ nói
cách khác sử dụng các định luật chuyển động của các yếu tố.
Khi có sự hình thành cấu trúc thì
đối xứng của hệ giảm đi, tính đồng nhất của hệ bị phá hủy hoặc entropy của hệ
trở nên nhỏ hơn.
Xác suất và entropy
Gọi X i tập các
trạng thái i = 1, 2, 3... W và p i = xác suất của
trạng thái X i . Theo
Boltzmann ta có entropy thống kê (statistical entropy) bằng
Trong đó k là hằng số
Boltzmann. Entropy thống kê là mức đo độ mất trật tự của hệ và cũng là số đo
cấu trúc tổ chức của hệ. Lúc S là
maximum ta có mức độ tổ chức thấp nhất của hệ.
Nếu tất cả p i = 1/W
(tất cả trạng thái đều đồng xác suất) ta có S = k ln W.
Một điều quan trọng là entropy thống
kê Boltzmann trùng với entropy nhiệt động học của Clausius [2a]. Cách chứng
minh H-định lý của Boltzmann dựa trên
phương trình động học vi mô ( kinetics ) cho phép giải thích được định luật
nhiệt động II từ quan điểm vi mô [2c]
(chú ý H = - S ).
Thuận nghịch & không thuận
nghịch (Reversibility & Irreversibility)
Trong nhiều trường hợp người ta phân
dS = d e S + d i
S , trong đó d e
S chỉ biến thiên entropy do sự trao
đổi nhiệt và vật chất với môi truờng bên ngoài còn d i S chỉ biến thiên của entropy do các biến
đổi nội tại của hệ. Luôn đúng hệ thức d i S ≥ 0 , nếu d i S = 0 ta có quá trình
thuận nghịch. Còn nếu d i S > 0 ta có quá trình không thuận nghịch. Đối
với các hệ kín d e S = 0 vậy
dS = d i S ≥ 0 .
Cân bằng & không cân bằng
(Equilibrium & Non equilibrium)
Như vậy đối với hệ kín entropy không
bao giờ giảm. Trạng thái cân bằng nhiệt động ứng với max của entropy : S
= max như vậy trạng thái cân bằng ứng với trạng thái với độ trật tự thấp
nhất.
Do đó những trạng thái ứng với
trình độ tổ chức cao (độ trật tự cao) phải là những trạng thái ở xa trạng thái
cân bằng S < S max. Đối với những
trạng thái xa cân bằng cũng luôn đúng hệ thức d i S > 0 và chú ý s
= sản lượng entropy (entropy production)
= d i S / dt
> 0 .
Hệ mở
Hệ mở là hệ có thể trao đổi với môi
trường bên ngoài năng lượng và vật chất.
Đối với hệ mở nội năng , số mol
cũng như entropy có thể tăng hoặc giảm mà không rơi vào mâu thuẫn với các
định luật nhiệt động học.
Sự thay đổi entropy dS có thể âm hoặc dương do tồn tại các
thông lượng vào và ra.
Trong các hệ mở
có thể tồn tại và hình thành những cấu trúc mà không mâu thuẫn với định luật 2
nhiệt động học. Việc hiểu các đặc tính của hệ mở và ý nghĩa sinh học
của chúng đã được hình thành trong các công trình của Schrodinger,
Bertalanffy, Prigogine, Wiame.
Cấu trúc phát tán (dissipative
structure)
Hãy xét các ví dụ sau đây.
a
/ Cấu trúc Bénard ( Bénard cells)
. Đây là một ví dụ điển hình về hiện tuợng tự tổ chức
Hãy đun một lớp chất lỏng và tạo nên
một ∆T
= T1 – T2
giữa mặt đáy và mặt thoáng của chất lỏng. Nếu T1 – T2 < ∆ T critical
thì chất lỏng nằm yên và ta chỉ có cơ
chế truyền nhiệt , song nếu ∆ T critical
< T1 – T2 thì xuất hiện đối lưu và phát sinh hệ
những ô mạng sáu cạnh Bénard.
Vì hệ chỉ trao đổi nhiệt với môi trường, cho
nên dòng entropy đi qua thành bình sẽ
được tính theo biểu thức (nhớ ∆S = Q/T ) : d e S
/ dt < 0 .
Như vậy hệ cung cấp entropy cho bên ngoài.
b
/ Ví dụ : phản ứng hóa học hữu
cơ do Belousov & Zhabotinski phát hiện năm 1950
:
Các kết quả thí nghiệm cho thấy rằng
với những nồng độ của các chất tham gia phản ứng (đóng vai trò thông số) lớn
hơn các trị số tới hạn thì có thể
quan sát được những hiện tượng sau đây : màu biến đổi chu kỳ từ đỏ ( nhiều ion Ce 3+ ) sang xanh (
nhiều ion Ce 4+ ) hoặc lúc đầu có sự thay đổi màu theo chu kỳ đỏ –
xanh - đỏ – xanh ...trong vòng 4 phút sau đó phát sinh nhiều lớp đỏ - xanh
chồng lên nhau một cách ổn định. Lúc đầu ta có cấu trúc dao động (cấu trúc
thời gian ) sau đó cấu trúc này biến
thành cấu trúc không- thời gian.
c
/ Mô hình brusselator
Sau đây ta xét các phản ứng hóa học
nghiên cứu bởi các tác giả Prigogine-Lefever . Ta gọi mô hình Prigogine-Lefever
là brusselator (tên mô hình xuất phát từ trường phái Brussels): điều quan trọng của mô hình này là sự
phát sinh các cấu trúc thời gian và không gian ( hiện tượng tự tổ chức)
Ký hiệu các concentration bằng chính
các ký hiệu trên .Đưa vào hai biến số x 1 & x 2 : X 1 = A + x 1 và X 2 = B / A
+ x 2
Viết lại hệ phương trình theo x
1 & x 2 sau đó tìm phương trình đặc trưng của hệ
phương trình . Từ đó ta có các kết quả sau. Lấy cố định A = 1 còn xem B như thông số
điều khiển. Trị số tới hạn là B critical = 2 . Tại B = B critical ta
có điểm rẽ nhánh , sau điểm đó sẽ có quỹ đạo giới hạn ổn định
(stabile limit cycle ). Xem hình 2a .
Khi B < B critical ta có các dao động lịm dần tiến đến một tiêu điểm ổn định
Khi B = B critical ta có điểm rẽ nhánh ( bifurcation )
Khi B > B critical ta có các quỹ đạo giới hạn.
Hình 2a
Trên đây ta thấy phát sinh hiện tượng tự tổ chức (self-organization) – với
cấu trúc thời gian . Sau đây ta xét đến hiện tượng tự tổ chức với cấu trúc không-thời gian của brusselator.
Ta giả sử hệ hóa học được phân bố
theo một đường thẳng dọc theo tọa độ r
.Bây giờ nếu xét thêm hiện tượng khuếch tán dọc theo r thì lời giải của hệ là :
Như vậy chúng ta có trạng thái biến
đổi có chu kỳ (cấu trúc theo thời gian)
và có dạng sinus ( cấu trúc không gian ).
Qua các ví dụ a,b & c chúng ta thấy được sự hình thành các cấu
trúc lúc hệ nằm ở vùng xa cân bằng . Hiện tượng
tự tổ chức xuất hiện khi các thông số vượt qua những trị số tới
hạn , lúc này các biến số của hệ tuân theo các phương trình phi tuyến.
Phi tuyến là tính quan trọng đối với các hệ ở xa cân bằng.
Prigogine gọi cấu trúc không- thời
gian ở xa cân bằng trong vùng phi tuyến khi các thông số của hệ
vượt qua các trị số tới hạn là cấu
trúc phát tán (dissipative structure).
Nhiệt động học không cân bằng
Quá trình không
cân bằng là quá trình dừng (stationary) với các điều kiện biên áp đặt vào hệ (
như nhiệt độ, áp lực, mật độ, ...) không cho phép hệ đi về trạng thái cân bằng .
Các trạng thái
dừng không xa
cân bằng lắm
Đối với những
trạng thái dừng không xa cân bằng lắm thì s
® min ( trạng thái dừng ổn định đối
với các nhiễu loạn nhỏ ), đó là định
lý Prigogine .
Các trạng thái
xa cân bằng nhiệt động. Nguyên lý Glansdorff-Prigogine.
(Phần này đặc biệt quan trọng đối với
sinh học).
Các cơ thể sống
là những hệ mở nhiệt động , ở rất xa trạng thái cân bằng . Trong đoạn này đại lượng đóng vai trò quan trọng là sản
lượng entropy s thay vì đại lượng entropy S.
Khi trạng thái dừng là cân bằng nhiệt động thì s = 0 còn nếu trạng thái dừng chỉ là trạng thái bền (steady),
không cân bằng nhiệt động thì s > 0. Khi s > 0 ta có hai loại trạng thái dừng (trạng thái bền tuyến
tính và cấu trúc phát tán) (xem hình vẽ 2b
). Trong vùng tuyến tính Prigogine chứng minh rằng hệ tiến triển theo
chiều hướng nhỏ dần của sản lượng entropy
s, đó là định lý Prigogine.
Khi hệ vượt qua
vùng tuyến tính và rơi vào vùng phi tuyến thì định lý Prigogine không còn đúng
nữa. Trong trường hợp bền tuyến tính các thăng giáng của các thông số chỉ tạo
nên những độ lệch dương của s đưa hệ trở về trạng thái dừng vì vậy
ổn định trong mọi trường hợp. Trái với điều đó trong vùng phi tuyến xa cân bằng
các thăng giáng của trạng thái dừng có thể dẫn đến những độ lệch âm của s , điều này làm cho hệ không ổn định.
Sự ổn định buộc điều kiện là chỉ chấp nhận những độ lệch dương của sản lượng
entropy. Đó là nguyên lý
Glansdorff-Prigogine. Sự chuyển từ vùng tuyến tính sang phi tuyến liên quan đến
sự hình thanh cấu trúc phát tán. Trong các cấu trúc cân bằng nhiệt động chỉ có
các cấu trúc không gian trong khi trong các cấu trúc phát tán chúng ta có thể
quan sát được cả những cấu trúc thời gian và cấu trúc trong continuum
không-thời gian
Hình 2b
3 . Hiện tượng tự tổ chức dưới quan điểm phức hợp
Khoa học phức hợp ( viết tắt là KHPH, tiếng Anh : complexity theory) là
môn khoa học nghiên cứu về các hệ phức hợp. Nói đơn giản, một hệ là phức hợp nếu nó chứa nhiều thành
phần con tương tác với nhau và nếu hệ đó lại biểu hiện những tính chất, những
lối hành xử (behavior) mà chúng ta không thể suy ra một cách hiển nhiên từ
tương tác của những thành phần cấu thành [3a].
Hiện nay chúng
ta đã có nhiều công cụ hữu hiệu như nhiệt động học (thermodynamics), cơ học
thống kê (statistical mechanics) để
nghiên cứu những hệ nằm trong
trạng thái cân bằng (equilibrium). Song những hệ cân bằng chưa phải hoàn toàn là những
hệ phức hợp. Tuy nhiên việc
nghiên cứu những hệ cân bằng sẽ cung cấp
nhiều khái niệm, nhiều ý tưởng cho việc nghiên cứu những hệ phức hợp, vốn là những hệ nằm ngoài trạng thái cân bằng.
Những hệ động
học nằm ngoài trạng thái cân bằng và do đó có tính phi tuyến mới là những hệ quan trọng trong vũ trụ. Những hệ phức hợp là: kinh tế, thị trường chứng
khoán, khí hậu thời tiết, các sinh vật và xã hội của chúng, môi trường, các
dòng chảy cuộn xoáy, dịch bệnh, nhịp đập của tim,... [3b]
Như vậy chắc
sẽ không có một lý thuyết đơn giản cho
các hệ phức hợp . Việc nghiên cứu các
hệ phức tạp đòi hỏi một sự tổng hợp liên
ngành (interdisciplinary). Đặc trưng quan trọng nhất của hệ phức hợp là gì?
Đó là hiện tượng đột sinh
(emergence) [3c]. Hiện tượng đột sinh là hiện tượng xuất hiện những quy
luật, những hình thái, những trật tự mới từ hiệu ứng tập thể của các tương tác giữa các thành phần của hệ
thống. Như vậy các hiện tượng đột sinh không phải là một tính chất nội tại của
các thành phần con mà là những tính chất của hệ thống được xét một cách toàn
cục. Hiện tượng tự tổ chức (self-organization) chủ yếu là một hiện tượng
đột sinh.
Các định luật
cơ học thống kê, nhiệt động học
Khi nghiên cứu
một hệ nhiều hạt người ta không thể sử
dụng tương tác vi mô giữa chúng để mô tả
toàn hệ mà phải cầu cứu đến các định luật của cơ học thống kê, nhiệt động
học. Đây là một minh họa về hiện tượng đột
sinh (emergence) khi lối hành xử của một hệ không thể suy từ hành xử của
từng hạt, của từng thành phần con.
Như thế có thể
nói cơ học thống kê, nhiệt động học là những khoa học cố điển nhất của lý
thuyết về phức hợp. Chúng ta đã thay thế cách tiếp cận quy giản luận, vốn là cách tiếp cận dựa
trên nhũng định luật vi mô tất định bằng cách tiếp cận thống kê và xác suất
đối với hiện tượng đột sinh.
Người ta thường
nói: toàn cục lớn hơn tổng cơ học các thành phần để biểu diễn hiện tượng
đột sinh. Và điều này cũng có nghĩa hệ
thống là phi tuyến , những hệ quả
bất ngờ đột xuất có thể xảy ra đối với một hệ thống phức hợp.
Cân bằng và không cân bằng (equilibrium
& non-equilibrium)
Một khái niệm quan trọng trong lý
thuyết về phức hợp là khái niệm tới hạn tự tổ chức (self-organised
criticality). Theo khái niệm
này các hệ phức hợp tự phát tiến triển về trạng thái tới hạn giữa
bất trật tự và trật tự.
Việc tiến đến
điểm tới hạn của quá trình tự tổ chức (self-organised criticality)
là nguyên lý mà các hệ không cân bằng sử dụng để tự tổ chức mình vào một trạng
thái nằm ở ranh giới bất trật tự (disorder) và trật tự (order).
Như vậy các hệ không cân bằng sẽ tự xếp
đặt mình vào một trạng thái tới hạn. Các tổ chức sống là những minh họa về
những hệ này.
Các tổ chức sống là những hệ phức tạp
nhất và một điều đáng lưu ý là các hệ
này phát triển đến một trật tự cao cấp trái ngược với chiều mũi tên thời
gian điều khiển bởi định luật thứ hai của nhiệt động học. Thật ra sự tăng độ
mất trật tự và entropy do định luật thứ hai của nhiệt động học chỉ áp dụng đối
với các hệ cân bằng kín. Các hệ sống không cân bằng và cũng không kín cần
một dòng năng lượng để làm tăng trật tự ( như vậy làm giảm entropy) cho
bản thân song lại phát tán nhiệt và các
chất thải để làm tăng bất trật tự (như thế làm tăng entropy) trong vũ trụ. Như
thế các hệ sống là những cấu trúc phát tán (dissipative structures) có khuynh
hướng tiến đến tự tổ chức (self-organisation).Các hệ phát tán không phải là
những hệ ở trạng thái cân bằng nhiệt động nhưng luôn có khuynh hướng tiến triển
về cân bằng nhờ dòng entropy và năng lượng.
Sự thoát khỏi
trạng thái cân bằng là cần thiết để cho một cơ thể sống có thể có được một trật
tự và hình thái phức hợp của nó.
Phức hợp & hỗn độn (Complexity
& chaos)
Phức hợp và hỗn độn là hai khái niệm
gắn liền nhau. Các hệ phức hợp nằm đung đưa ở
ranh giới giữa hỗn độn và trật tự (balanced on the edge of chaos – not
too orderly, not too disorderd). Cho nên việc nghiên cứu phức hợp gắn liền với
lý thuyết hỗn độn.
Lý thuyết hỗn độn mô tả lối hành xử
của một số hệ động học phi tuyến rất
nhạy cảm với điều kiện ban đầu. Vì sự nhậy cảm này mà lối hành xử của hệ dường
như hỗn độn, mặc dầu động học của nó được mô tả một cách tất định bởi
những hệ phương trình vi phân.
Hiện tượng
trong đó một hệ hoàn toàn tất định có thể dẫn đến những hệ quả không tiên đoán
được gọi là hỗn độn.
Các trạng thái
của hệ phức hợp thường có thể mô tả bởi một hệ phương trình vi phân phi tuyến
nối liền các đại lượng X 1, X 2, X 3, ... ( như nhiệt độ, áp suất, ...và một số
tham số a 1, a 2,
a 3,... (như số Prandtl, số Rayleigh,...là những thông số kỹ
thuật). Hệ phương trình này xác định cách hành xử của hệ phức hợp. Một điều
kiện cần (chưa phải là đủ) cho hỗn độn là tính phi tuyến của hệ thống.
Hỗn độn là một tính chất của các hệ động học phi
tuyến, đó là tính siêu nhậy cảm đối với
các điều kiện ban đầu. Cho nên các hỗn độn quan sát được thật ra là hệ quả của
một trật tự nằm trong không gian pha (X 1, X 2,
X 3, ...) tức không gian
của các trạng thái (trong cơ học không gian pha là không gian tọa độ-xung
lượng). Mỗi điểm trong không gian pha ứng với một trạng thái của hệ, các điểm
đó làm thành quỹ đạo trạng thái. Nhiều hiện tượng tưởng chừng như
ngẫu nhiên song đó là những hỗn độn
của một hệ tất định.
Phần của không
gian pha ứng với một hành xử nhất định của hệ phức hợp làm thành tập hút
(attracting set) hay nói cách khác làm thành quỹ đạo hút (attractor) .
Tâm hút trong
các hệ phát tán
Quỹ đao hút có
chu kỳ (periodic attractor)
Quỹ đạo hút có
chu kỳ là một vòng lặp lại của các trạng thái. Ví dụ quỹ đạo của một hành tinh
quanh một sao là một quỹ đạo hút có chu kỳ=1. Trên hình 3a là một quỹ đạo hút
với chu kỳ = 4.
Hình 3a
Quỹ đạo hút lạ
(strange attractor)
Tính nhậy cảm
đối với điều kiện ban đầu được biểu hiện ở sự phân kỳ các quỹ đạo trong không
gian pha. Đối với các hệ phát tán khái niệm hỗn độn gắn kiền với khái
niệm quỹ đạo hút lạ (strange attractor ):
vì có hỗn độn cho nên các điểm mô tả trạng thái không nằm trên một quỹ đạo hút
bình thường ví như quỹ đạo của một hành tinh quanh một sao, mà nằm trên một quỹ
đạo hút lạ.Chuyển động hỗn độn dẫn đến những quỹ đạo hút lạ (strange attractors).
Quỹ đạo hút lạ là một quỹ đạo hút không
có chu kỳ biểu hiện của hỗn độn. Một ví dụ được minh họa ở hình 3b .
Hình 3b . Quỹ đạo hút lạ
Không đi sâu vào định nghĩa toán học ,
chúng ta hãy xác định số chiều D của quỹ đạo hút lạ trên hình 3b. Ta thấy các vòng
này dày đặc chiếm gần hết không gian 3
chiều nhưng không chiếm hết! Mặt khác
chúng cũng chiếm nhiều chỗ hơn không gian 2 chiều vì thế số chiều
(dimension) của tâm hút này là 2 < D < 3. Đó là một đặc trưng
của fractal: có số chiều D không nguyên.
Hai loại tâm hút có chu kỳ (periodic) và lạ
(strange) được quan sát trong các hệ phát tán.
Sự tiến hóa
sinh học và lý thuyết tai biến
Lý thuyết tai
biến (catastrophe theory, viết tắt là LTTB ) nghiên cứu và xếp loại các hiện
tượng đột biến của một hệ động học gây nên bởi những nhiễu loạn ngoài. Với sự phát triển của khoa học phức hợp
(complexity science) hiện đại trong thế kỷ 21, LTTB hội nhập như một cách tiếp
cận độc đáo, sáng tạo.
Lý thuyết tai biến
Lý thuyết tai
biến được René Thom (Fields 1958) phát triển vào những năm đầu thập kỷ 70
trước. LTTB được trình bày trong cuốn
sách nổi tiếng của René Thom “ Ổn
định cấu trúc và tạo sinh hình thái, Structural Stability and Morphogenesis
“ [3d]. Chữ morphogenesis có từ nguyên Hylạp morphe-hình thái và genesis-tạo sinh có nghĩa là quá trình
tạo hình thái (từ phôi -embryo), một quá trình cơ bản trong sinh học.
Lý thuyết tai biến cung cấp cho chúng ta một cách nhìn và mô tả thế giới
có khả năng làm xuất hiện những điểm dị đồng giữa những hiện tượng và hình thái
rất xa lạ của tự nhiên.
Trong [3d] René Thom đưa ra những
khái niệm sau:
1 /
Mỗi đối tượng hay nói cách khác mỗi hình thái vật lý được mô tả bởi một
tập hút trong không gian trạng thái các biến số trong.
2
/ Đối tượng ổn định
chỉ trong trường hợp tập hút tương ứng là ổn định cấu trúc.
3
/ Mọi tạo sinh hình thái (morphogenesis) có thể mô tả
bởi sự biến mất của tập hút trong dạng thái ban đầu để được thay thế bởi tập
hút mới trong dạng thái cuối cùng. Quá trình này gọi là tai biến và được
mô tả trong không gian các biến số ngoài.LTTB được xem như bộ phận của lý thuyết hỗn độn (chaos
theory).LTTB hội nhập vào KHPH như một
mốc phát triển quan trọng và một công cụ hữu hiệu không thể vắng mặt trong khoa
học phức hợp cùng với các lý thuyết khác như fractal,
lý thuyết hỗn độn (chaos theory) .
Quan điểm của
René Thom về sinh học
René Thom
nghiên cứu vấn đề tạo sinh hình thái
(morphogenesis) trong sinh học. Như chúng ta thấy khoảng cách dường như không
rút ngắn được giữa vật lý cổ điển và những bí ẩn của quá trình phát triển phôi ( embryogenesis) đã
dẫn các nhà sinh học lỗi lạc thế kỷ XIX đến thuyết sức sống (vitalism).
Hiện nay thuyết neo-darwin (tổng hợp thuyết tiến hóa Darwin và di truyền học phân
tử ) có thể cung cấp một cách nhìn đối với vấn đề sinh học. Song lý thuyết
néo-darwin không cho phép hiểu được các biểu hiện hình thái vĩ mô . Lý
thuyết neo-darwin thực chất là một lý thuyết thuộc loại quy giản luận (dựa trên
những cơ sở tương tác vật lý- hóa học vi mô). Như vậy thuyết neo-darwin cần
được bổ sung bởi những lý thuyết về cấu trúc hình thái . Cơ thể không phải chỉ
là một hệ vật lý – hóa học mà là một cấu trúc nghĩa là một hệ có những mối liên
quan nội tại thỏa mãn những định luật hình thức. Điều này dẫn đến những vấn đề
như ổn định cấu trúc. Vì những lý do đó mà René Thom đưa ra một tiếp cận cấu
trúc đối với những quá trình biến đổi hình thái sinh học. Sự ổn định cấu trúc
sẽ làm phát sinh những nhánh phân rẽ ( chuyển pha) và tôpô của các tập hút.
Rene Thom phát
biểu rằng “ Một trong những bài toán trung tâm cho trí tuệ chúng ta là tìm hiểu
sự chuyển biến (sinh ra, phát triển, chết đi, ổn định và biến đổi ) của các
hình thái . René Thom muốn nói đến một bản thể học định tính (ontology
qualitative), một kết hợp giữa sinh hóa học và tôpô (mix of biochemistry and
topology).
Bảy tai biến cơ
bản
Những hiện
tượng dễ đập vào giác quan chúng ta, chính là tập những điểm kỳ dị mà trong vật
lý học người ta gọi là những điểm tới hạn, ví dụ các điểm tới hạn trong lý thuyết chuyển
pha. Tại những điểm đó trạng thái của hệ đột biến, nói cách khác, hệ nhảy
từ trạng thái này sang trạng thái khác một cách gián đoạn, ví dụ từ trạng thái
lỏng sang trạng thái rắn, Nhũng hiện tượng đột biến có tên là tai biến
(catastrophe) trong LTTB của René Thom. Chữ tai biến mà René Thom sử
dụng chỉ có ý nghĩa toán học.
Trong LTTB
người ta đưa vào khái niệm ổn định cấu trúc để diễn tả tính ổn định của hình thái các
tai biến dưới tác động của những nhiễu loạn không điều khiển được.
Các hiện tượng
và hình thái của thiên nhiên rất đa dạng đến mức ta khó lòng nắm được mối liên
quan giữa chúng. Có điểm gì giống nhau giữa các hiện tượng quang học và một
hiện tượng tâm lý? Câu hỏi tưởng chừng như vô nghĩa, nhưng LTTB cung cấp cho chúng ta một cách mô tả làm
nổi lên những điểm dị đồng giữa nhiều hiện tượng và hình thái.
René Thom tìm
ra được 7 tai biến cơ bản (hình 3c), theo đó có thể xếp hạng nhiều hiện tượng
và hình thái trong thiên nhiên, và như vậy cho chúng ta thấy được mối liên quan
ví dụ giữa một hiện tượng tâm lý với một hiện tượng quang học. Có thể nói LTTB
là một bài thơ thất ngôn tuyệt đẹp về nhiều hiện tượng và hình thái của thiên
nhiên.
Hai biến số
trong N & bốn biến số ngoài C
Những phương
pháp tính toán do Leibnitz và Newton đề ra chỉ ứng dụng được cho những hiện
tượng liên tục. Những hiện tượng đột biến đòi hỏi những lý thuyết mới. Khi
nghiên cứu một hệ trong môi trường người ta thấy có hai trường hợp. Trong
trường hợp thứ nhất sự tương tác của hệ với môi trường được mô tả bởi một
hàm thế V của các biến số trong X1,X2,X3,
... chỉ trạng thái của hệ và các biến số ngoài a1, a2,
a3, ... chỉ môi trường.
Ngoài ra ta có một hệ phương trình vi phân cho V. Hệ sẽ ở vào những
trạng thái ứng với các cực tiểu địa phương, nghĩa là những điểm ở đấy V
nhỏ nhất so với vùng lân cận. Những điểm đó thuộc về những điểm tới hạn của hàm
V. LTTB với giả thiết có tồn tại một hàm thế có thể gọi là LTTB hẹp.
Trong trường
hợp thứ hai ta không có một hàm thế như trên và phải sử dụng nhiều công
cụ toán học tổng quát hơn lý thuyết phương trình vi phân. LTTB không hàm thế
gọi là LTTB rộng.
Trong LTTB hẹp
người ta công nhận sự tồn tại một hàm thế và một hệ phương trình vi phân song
không đặt vấn đề giải hệ phương trình vi phân ấy vì đó là một việc làm quá khó khăn lúc số biến
số quá lớn. Vậy LTTB sử dụng cách tiếp cận nào và dẫn đến những kết luận gì?
Hình 3c . Bảy tai biến trong LTTB của René Thom xếp từ trên xuống dưới, bên trái : nếp xếp, nếp gấp lùi, đuôi én, bướm, bên phải: rốn hyperbolic, rốn elliptic, rốn parabolic.
Đối với một hàm có kỳ dị ta có thể
tìm được một hệ tọa độ trong đó ta có thể phân hàm thành hai phần Q và
G: Q là một dạng toàn phương không suy biến, còn G chứa số
biến số còn lại. Hàm G gọi là kỳ dị thặng dư và số biến số trong
G gọi là đối hạng của kỳ dị. Chỉ hàm G mới quan trọng về mặt
tôpô và ứng với những hàm G khác nhau ta có những loại kỳ dị khác nhau.
Hàm G chưa ổn định. Đem nhiễu loạn hàm G ta có những hàm mới chứa
thêm các biến số ngoài a1, a2, a3, ...Các hàm này có tính ổn định cấu trúc,
có nghĩa là khi chúng bị nhiễu loạn, hình học của hiện tượng vẫn không thay
đổi. Các hàm có tính ổn định với số biến số ngoài nhỏ nhất đóng vai trò hàm thế nói trên. Như vậy mỗi
mầm hàm có hai đặc trưng quan trọng là:
-
đối hạng N tức số biến số trong còn lại trong kỳ dị thặng
dư và
-
đối chiều C tức số biến số ngoài đưa vào với mục đích thu
được một hàm ổn định dưới các nhiễu loạn.
Chiếu tập những điểm tới hạn của hàm
V xuống không gian các biến số ngoài a1,
a2, a3, ... ta
có các hình thái đặc trưng cho các tai biến (xem hình 3c).
Hạn chế N ≤ 2 và
C ≤ 4, René Thom tìm ra được 7 tai biến cơ bản. Các tai biến đó có ký hiệu
(N,C):
1
/ nếp xếp (1,1) – fold
catastrophe
2
/ nếp gấp lùi (1,2) – cusp catastrophe
3
/ đuôi én (1,3) – swallowtail
catastrophe
4
/ bướm (1,4)- butterfly catastrophe
5
/ rốn hyperbolic (2,3)- hyperbolic
catastrophe
6
/ rốn elliptic (2,3)- elliptic
catastrophe
7
/ rốn parabolic (2,4)- parabolic
catastrophe
Chú ý số chiều của không gian ta
sống bằng 4: ba chiều thời gian và một chiều thời gian, liệu có mối liên quan
với hạn chế C = 4 trong LTTB của René Thom?
Khi xét một hệ trong thực tế, chúng
ta thường phải đưa vào một số biến số trong rất lớn. Trong LTTB của René Thom
ta thấy N ≤ 2 , điều đó có nghĩa rằng về mặt tai biến chỉ có 2 trong số biến số
trong mô tả trạng thái của hệ là quan trọng.
Như thế LTTB cho ta hiểu được sự
phát triển của hệ mà không cần giải một hệ phương trình vi phân với số biến số
quá lớn, nói cách khác LTTB công nhận một tất định luận (determinism) ẩn
mà không đặt mục đích tìm ra tường minh tất định luận đó.
Làm thế nào để tìm ra tai biến của một hiện tượng?
Muốn biết một
hiện tượng thuộc loại tai biến nào, chỉ cần tìm hàm V, xong tìm các điểm
tới hạn của V theo các biến trong, rồi chiếu chúng xuống không gian các
biến ngoài thì thu được tai biến của hiện tượng.
Sự biệt hóa tế bào trong sinh học
[3e]
Sau đây là một trong nhiều ví dụ áp
dụng LLTB vào sinh học: lý thuyết Zeeman
về sự biệt hóa tế bào . Zeeman xét một mô hình đơn giản về sự hình thành các tổ
chức cơ và xương từ những tế bào hoàn toàn giống nhau trong quá
trình phát triển của phôi. Giả sử rằng các tế bào làm thành một tập các hệ đồng nhất với nhau điều khiển bởi nồng
độ địa phương của một số chất hóa học.
Lấy một cơ thể một chiều trong đó
các tế bào phân bố dọc theo trục Ox
(hình 3d).
Biến số duy nhất là Q mô tả tỷ lượng tế bào
“xương” trong quá trình biệt hóa. Khi Q < m ta có các tiền
tế bào với tổ chức cơ . Khi Q tiến đến trị số b ta sẽ có các tiền tế bào với tổ chức xương
. Khi quá trình phân chia hoàn thành Q nhảy vọt từ trị số M (
ứng với tổ chức cơ) sang trị số B ( ứng với tổ chức xương )
Các tế bào với x <
x C sẽ phát triển liên tục và tạo thành các tổ chức cơ
tại điểm M . Các tế bào ứng với x
C <
x < x A thực hiện một bước nhảy
động học ( rất có thể dưới tác động của “ một chương trình gen “ ). Sau điểm x A tế bào phát
triển thành các tổ chức xương. Điểm A là một điểm phân nhánh ứng với một
gia số rõ rệt của Q.
Trên mặt (x, t) ta nhận thấy
được tai biến “ nếp gấp lùi ” .
Hình 3d
. Trên hình vẽ giả sử rằng các tế bào của phôi được phân bố dọc theo
trục x . Với các trị số nhỏ của x các tế bào phát triển thành các tổ chức cơ ,
với các trị số x lớn – thành các tổ chức xương. Đại lượng Q mô tả tỷ lượng tế
bào “xương” . Zeeman mô tả hiện tượng như tai biến “nếp gấp lùi ” .
Các nhà vật lý
lý thuyết cho rằng không có lý thuyết nào đẹp đẽ và tổng quát như LTTB trong
lúc nghiên cứu các kỳ dị . Và nếu nói đến một văn hóa trong nhận thức
luận nói chung của nhân loại thì LTTB là một tiếp cận vấn đề phức hợp độc đáo và sáng tạo.
4 . Lý thuyết lượng tử và vũ trụ học với
sinh học
Nhiều thế kỷ
trước các cơ thể sống được xem như là một loại vật chất có ma thuật (magic
matter), song có thể đó chỉ là vật chất như mọi vật chất với những tính chất
đột sinh mà chúng ta chưa nắm được quá trình phát triển.
Những hiện
tượng lượng tử : tính gián đoạn, hiện tượng đường hầm (
tunnelling), tính chồng chất ( superposition) , hiện tượng liên đới
lượng tử ( quantum entanglement) đã dẫn đến những kết quả quan trọng ( ví
dụ đã được ứng dụng trong các máy tính lượng tử ) đã và sẽ phải được ứng dụng
vào sinh học. Sự sống đã để gần 3,5 tỷ năm để tiến đến hiện trạng ngày nay chắc
đã phải trải nghiệm qua những hệ quả tinh diệu của lượng tử.
Hiện nay sinh
học đang phát triển ở mức phân tử cho nên lý thuyết lượng tử không thể không
đóng vai trò quan trọng vào sinh học. Viên gạch cơ bản trong sinh học là acid
nucleic DNA gồm hai dãy
polynucleotide xoắn quanh nhau và nối liền nhau bởi các cặp cơ sở (base pairs): A(Adenine),
T (Thymine), G (Guanine), C (Cytosine), T đi cặp với A còn G đi
cặp với C (hình 4a).
Hình
4a . Mô hình cấu trúc DNA
Nhờ hiệu ứng đường
hầm trong lý thuyết lượng tử mà có thể xảy ra trường hợp T không đi
cặp với A mà có thể đi cặp với G, điều này dẫn đến hiện tượng đột biến ( mutation) , như vậy thuyết lượng
tử chắc chắn có đóng vai trò quan trọng trong sự tiến hóa sinh học.
Alexei
Kornyshev ( College Hoàng gia Anh ) nghĩ rằng trong thế kỷ XXI nhiều điều kỳ
diệu trong sinh học có thể chờ đón từ vật lý (lượng tử và cổ điển).Tuy nhiên
Adrian Parsegian, một nhà lý-sinh học Mỹ cho rằng hiện nay cũng còn nhiều chướng
ngại trong việc kết hợp vật lý học với sinh học thứ nhất vì độ phức tạp lớn của
các cơ thể sống và thứ hai vì quan điểm và công cụ khác nhau từ hai phía nên
khó lặp lại dược một cộng tác hữu hiệu giữa nhà vật lý và nhà sinh học như
trong trường hợp James D.Watson (sinh học ) và Francis Crick ( vật lý) khi đưa
ra mô hình cấu trúc DNA. Tuy nhiên cũng cần nhắc đến truờng hợp dưới đây
của Roger Penrose và Stuart Hameroff.
Một đột sinh
quan trọng : đột sinh ý thức (consciousness) từ hệ tế bào thần kinh. Lý thuyết
lượng tử có thể có khả năng tìm ra mối liên quan giữa tinh thần ( mind )
và não bộ (brain) và nói riêng là tìm
hiểu sự đột sinh của ý thức. Một trong nhiều mô hình đã được Roger Penrose
& Stuart Hameroff xây dựng để giải thích sự đột sinh của ý thức bằng một
hiện tượng có tác động vĩ mô lên não bộ.
Sau đây là sơ
đồ đơn giản hóa mô hình
ORCH-OR (Orchestrated Objective
Reduction) của Roger Penrose & Stuart Hameroff. Như chúng ta biết khi tiến
hành một phép đo thì hàm sóng của hạt lượng tử
chịu một phép co (collapse) gọi là SR (Subjective Reduction) .Năm 1993
Henry Stapp đưa ra giả thuyết là nếu có những phép co lượng tử
trong não bộ thì đó là một ví dụ
của ý thức . Roger Penrose (một nhà vật lý lý thuyết ) giả định một loại
lượng tử trong não bộ, cô lập với môi
trường, không co lại vì một phép đo nào cả mà tự co lại , phép co đó được gọi
là OR (Objective Reduction). Song Penrose chưa làm sáng tỏ một điều là giá đỡ
(support ) của quá trình này là vật gì trong não bộ.
Stuart Hamaroff
(một nhà gây mê) đã gợi ý về một số cấu trúc trong tế bào có thể đảm đương
nhiệm vụ đó. Đó là các microtubules ( thành phần quan trọng của cytoskeleton).
Microtubule (xem hình 4b) là những ống hình trụ rỗng trong tế bào nối liền với
nhau bởi những protein liên kết (MAP-Microtubule Associated Proteins ).
Hameroff cho rằng các electron tồn tại trong các tubulin (protein cấu tạo nên
microtubule) có thể liên kết với nhau trong trạng thái một ngưng tụ
Bose-Einstein ( Bose-Einstein condensate) , các condensate trong những microtubules
của một neuron có thể nối liền với các neuron khác nhờ hiệu ứng đường hầm.
Hameroff giả định rằng hiệu ứng đường hầm cho phép một thực thể lượng tử như
các condensate nói trên lan truyền đến nhiều neuron khác và trải rộng trong một
vùng lớn của não bộ như một thực thể lưọng tử thống nhất . Chính hiện tương OR
của thực thể lượng tử kết hợp này được
chỉ huy hiệp đồng như trong một bản hòa tấu nhờ các MAP sẽ tạo ra ý thức. Vì thế mô hình của Penrose
- Hameroff được đặt tên là ORC-OR (Orchestrated Objective Reduction – Phép co
Khách quan Hiệp tấu ). Mô hình của Penrose và Hameroff là một gợi ý dùng lý
thuyết lượng tử vào sinh học cụ thể là tiếp cận một trong những vấn đề lớn của
sinh học: sự đột sinh của ý thức từ hệ tế bào thần kinh. Mô hình ORC-OR của
Penrose & Hameroff là một mô hình
được nhiều nhà vật lý chú ý song cũng là
một mô hình chưa có được một kiểm nghiệm thực tế nào và chịu nhiều sự phê phán
từ phía các nhà triết học và khoa học khác.
Hình 4b . Sơ đồ
vùng trung tâm của neuron cho ta thấy những microtubule nối liền với nhau bởi
các MAP
Tự tổ chức
(self-organization) trong vũ trụ
Các tác giả Jerzy
Jurkiewicz, Renate Loll and Jan Ambjorn đã công bố một bài viết lý thú lấy tên
là “ Vũ trụ lượng tử tự tổ chức “ ( The Self- organizing Quantum Universe)
[4a]. Lẽ dĩ nhiên ở đây các tác giả không dùng lý thuyết động học vi
mô (kinetics theory) để xây dựng nên vũ trụ lượng tử tự tổ chức mà
phải sử dụng thuyết lượng tử và hấp dẫn . Song điều đáng nói ở đây là ý
tưởng về hiện tượng tự tổ chức của vũ trụ được lấy từ ý tưởng về hiện tượng tự tổ chức trong sinh
học , từ ý tưởng đột sinh trong lý thuyết phức hợp ( complexity).
Các tác giả đã lấy các “tế bào” cơ
bản là những đơn hình (simplex) thỏa mãn điều kiện nhân quả tương tác với nhau
qua hấp dẫn và lượng tử. Các tế bào này sẽ tự sắp xếp ( tự tổ chức ) để tạo nên
vũ trụ mà chúng ta quan sát được . Những tế bào
hay “ nguyên tử “ mà các tác giả sử dụng là những tam giác suy rộng
4-chiều. Các tác giả đã gán cho mỗi đơn hình một mũi tên thời gian hướng từ
quá khứ đến tương lai sau đó dán dính chúng với nhau sao cho mũi tên thời gian
chung không thay đổi hướng ( xem hình 4c
) nhằm bảo đảm tính nhân quả của vũ trụ tạo thành. Lý thuyết này được
các tác giả gọi là CDT (Causal Dynamical Triangulations- Tam giác hóa Động
học Nhân quả ) . Lý thuyết CDT có nội dung tương đồng với Loop Quantum Gravity ( LQG
- Hấp dẫn Lượng
tử Vòng ) của Lee Smolin. Có thể nói các tam giác suy rộng 4
chiều này cũng là một loại phân tử “DNA”
của vũ trụ. Một chi tiết đáng chú ý là Jurkiewicz, một trong ba tác giả , là
Giám đốc bộ môn lý thuyết các hệ phức hợp tại Viện Vật lý thuộc Đại học
Jagiellonian ở Krak.
Hình 4c. Các tế bào đơn hình thỏa mãn điều kiện nhân
quả tự tổ chức thành vũ trụ
Đặc biệt thú vị là những ý kiến của
Leonard Susskind, Đại học Stanford [4b].
Susskind cho rằng tuy Darwin không quan tâm đến vũ trụ học song ngoài ý muốn của Darwin, chúng ta có thể phát
triển mối tương đồng giữa học thuyết
Darwin với các lý thuyết về vũ trụ. Darwin và Wallace nhấn mạnh đến hiện
tượng đột biến (mutability) và quy tắc chọn lọc tự
nhiên (natural selection) như là những động lực chính của tiến hóa. Song ở
đây theo Susskind tồn tại một điều còn cơ bản hơn cả hai điều vừa nói . Đột
biến và chọn lọc tự nhiên sẽ khó lòng
tạo nên một cơ thể sống như con người nếu không có yếu tố quan trọng sau này : đó là con
số khổng lồ trong phong cảnh các thiết kế sinh học ( the enormity of the
landscape of biological designs ). Danh từ phong cảnh (landscape)
lấy từ lý thuyết dây ( string theory) [4c].
Các thiết kế sinh học được mã hóa trong các phân
tử DNA, gồm hai dãy polynucleotide xoắn quanh nhau và nối liền nhau bởi
các cặp cơ sở A, G, C & T.
Trong một cơ thể mỗi phân tử DNA có thể chứa nhiều triệu cặp cơ sở. Số
khả năng chọn cặp cơ sở xác định nên phong cảnh sinh học và số khả năng đó vô cùng lớn. Một trăm triệu cặp cơ sở có thể
cho ta 4 100 000 000 cách sắp
xếp.
Giả sử ta chỉ
có một nghìn thậm chí một triệu thiết kế thử hỏi xác suất để một thiết kế đó
tạo nên một cơ thể có trí tuệ là bao
nhiêu ? Hoàn toàn không đáng kể. Song nếu số thiết kế đó là 4 100 000 000 tổ hợp thì tình huống đã khác vì xác suất đó
đã trở lớn hơn nhiều. Như vậy nguyên lý đầu tiên của tiến hóa sinh học – thậm
chí còn cơ bản hơn cả nguyên lý chọn lọc tự nhiên - đó là quy mô khổng lồ của phong
cảnh các thiết kế sinh học, theo ý kiến của Leonard Susskind, một nhà vật
lý lý thuyết dây.
Ta quay trở lại
các “DNA” của vũ trụ. Theo lý thuyết dây (string theory) không thời gian ngoài
bốn chiều thông thường còn có 6 hoặc 7 chiều dư ( extra dimensions ).
Như vậy ngoài 4 chiều không thời
gian những chiều dư (10 – 4 = 6 chiều) đã cuộn lại (compắc hóa ) thành một đa
tạp 6D có cấu trúc nhất định mang tên đa tạp Calabi-Yau do đòi hỏi bởi một số
điều kiện vật lý (hình 4d).
Không gian các chiều dư (extra
dimensions) có thể có nhiều dạng (nhiều tôpô): hình cầu , hình xuyến, hai hình
xuyến giao nhau tạo nên những tay quai (handles), và v.v...Ngoài ra phải kể đến
những thông số như độ dài tay quai, tiết diện tay quai, vị trí các màng,
số thông lượng quấn quanh các vòng... (xem hình 4d).
Hình
4d . Trên hình là bức tranh phong cảnh biểu diễn năng lượng theo 2 thông số .Đa
tạp các chiều dư ( đa tạp Calabi-Yau) được biểu diễn tại đáy các thung lũng ứng
với một chân không bền (ổn định) tương đối .
Các kiểu compắc
hóa dẫn đến 10 500 phương án, số phương án này còn lớn hơn cả số
nguyên tử trong toàn vũ trụ! Điều này dẫn đến một phong cảnh [ 4b] (danh
từ của Leonard Susskind ) có đồi núi với 10 500 thung lũng ứng với
chân không.
Đa tạp
Calabi-Yau giống như cột sống của phân tử DNA và các thông số nói
trên được sắp xếp theo vô số khả năng (tương tự như trong một phân tử sinh học
DNA).
Nếu các chi tiết của DNA xác định các tính
chất sinh học của một cơ thể sống, thì các thông số nói trên (và các yếu tố khác) xác định các
tính chất của vũ trụ.
Khi bàn đến mối
tương đồng với tái sinh (reproduction) và đột biến (mutation), thì lý thuyết lạm phát vũ trụ sẽ
vào cuộc. Trong quá trình lạm phát nhiều
vũ trụ sẽ được tạo ra với những định luật vật lý, những hằng số khác nhau
giống như cây rẽ nhánh của sự sống
(tree of life). Như vậy thuyết lạm phát trong vũ trụ chính là hiện tượng tương
tự của tái sinh và đột
biến trong sinh học.
5 . Vũ
trụ toàn ảnh : Sự liên thông giữa hai
vương quốc không sống (non-living) và sống (living)
Toàn ảnh ( holography) là gì ?
Như chúng ta biết trong quang học có
phương pháp ghi một vật thể 3 chiều bằng một ảnh 2 chiều (hologram).
Kỹ thuật này gọi là holography (phương pháp
toàn ảnh). Chữ holography có gốc từ tiếng Hy lạp holos- whole, toàn thể + graphe- writing, ghi ảnh. Đây là một
phương pháp chụp ảnh hiện đại. Holography được phát minh năm 1948 bởi nhà vật
lý người Hung Dennis Gabor (1900-1079, Nobel 1971).
Hologram là một ảnh 2D (2 chiểu),
song khi được nhìn dưới những điều kiện chiếu sáng nhất định thì tạo nên một
hình ảnh 3D (3 chiều) trọn vẹn. Mọi thông tin mô tả vật thể 3D đều được mã hoá
trên mặt biên 2D. Như vậy chúng ta có hai thực tại 2D và 3D tương đương với
nhau về mặt thông tin (xem hình 4a).
Một tính chất quan trọng khác của
hologram là nếu chỉ lấy một phần của nó người ta cũng có thể khôi phục được
hình ảnh 3D của vật.
Hai kiến trúc
sư lớn của toàn ảnh
Hai nhà khoa
học, kiến trúc sư của lý thuyết toàn ảnh là: nhà vật lý David Bohm (Đại học London) và nhà thần kinh
học xuất sắc Karl Pribram (Đại học Stanford , tác giả cuốn sách nổi tiếng Các
ngôn ngữ của não bộ – Languages of the Brain). Một điều kỳ lạ là hai nhà
khoa học này vốn làm việc trong hai lĩnh vực hoàn toàn khác nhau lại cùng đi
đến những kết luận giống nhau. Bohm đi đến kết luận về tính toàn ảnh của
vũ trụ sau nhiều năm không hài lòng với những giải thích các hiện tượng vi mô
theo thuyết lượng tử, còn Pribram - vì sự thất bại của các lý thuyết cổ điển
sinh học đối với những bí ẩn trong sinh lý học thần kinh ( neurophysiology).
Cuối cùng họ
gặp nhau và cùng hiểu rằng mô hình toàn ảnh cho phép hiểu được một loạt
những điều bí ẩn trong vật lý, trong thần giao cách cảm (telepathy), tiên tri
(precognition-biết trước sự vật), sự thống nhất con người và vũ trụ (oneness),
động học tâm lý (psychokinesis),...
Vũ trụ là một toàn ảnh (hologram)
Nguyên lý toàn ảnh có thể dẫn
đến một triết học sâu sắc. David
Bohm quan niệm rằng thực tại mà chúng ta
tiếp xúc hằng ngày chỉ là một loại ảo tưởng giống như một bức tranh toàn ảnh
(hologram). Dường như thực
tại có hai mức: một mức ở sâu hơn gọi là mức tiềm ẩn (cuộn lại), implicate (enfolded)
và một mức gọi là mức tường minh (mở
ra), explicate (unfolded). Một film
toàn ảnh (hologram) và hình ảnh nó tạo ra là ví dụ của hai mức tiềm ẩn và tường minh. Cuộn film thuộc mức tiềm
ẩn vì hình ảnh được mã hóa trong các dạng giao thoa chứa trong film còn hình
ảnh chiếu ra thuộc mức tường minh vì các giao thoa mã hóa được mở ra (unfolded).
Theo David Bohm
sóng và hạt đều bị cuộn lại trong một thực thể lượng tử, chỉ có quá trình tương
tác mới bộc lộ tường minh một khía cạnh
nào đó còn khía cạnh kia vẫn nằm tiềm ẩn. Vì từ toàn ảnh (holographic)
có tính tĩnh tại (static) nên để mô tả những quá trình động (dynamic) cuộn lại
và mở ra liên tục của thực tại nên David Bohm đưa ra danh từ toàn ảnh động
(holomovement)
Bohm quan niệm
rằng mọi vật trong vũ trụ đều là những phần tử của một continium [4a]. Bohm
cho rằng phân biệt thế giới sống (living) và không sống (nonliving) là điều vô
nghĩa.
Vì mỗi phần của
một bức toàn ảnh (hologram) đều chứa thông tin của toàn ảnh cho nên mỗi bộ phận
của vũ trụ đều chứa thông tin của toàn vũ trụ. Điều đó có nghĩa là nếu biết
cách tiếp cận thì chúng ta có thể tìm thấy thiên hà Tiên nữ (Andromeda) trong
móng ngón tay bàn tay trái [4b].
Não bộ là một toàn ảnh (hologram)
Pribram xuất phát từ việc tìm hiểu
não bộ lưu trữ trí nhớ bằng cách nào và ở đâu . Trong những năm 1940 người ta
tin rằng trí nhớ nằm trong não bộ. Mỗi dấu vết trí nhớ gọi là một engram, tuy
chẳng ai biết engram được cấu tạo bằng gì .
Từ năm 1920 Wilder Penfield dường
như chứng minh được rằng các engram nằm trong những vùng nhất định của não bộ .
Pribram, lúc còn là một nhà phẫu thuật thần kinh nội trú không có một nghi ngờ
nào đối với lý thuyết engram của Penfield. Song nhiều điều xảy ra đã làm
Pribram thay đổi quan điểm. Tại Phòng thí nghiệm sinh học Yerkes, Florida, nhà tâm lý thần kinh (neuropsychologist) Karl
Lashley đã huấn luyện chuột một số kỹ năng rồi cắt bỏ những phần trong não bộ
có thể liên quan đến kỹ năng đó (không một nhà phẫu thuật nào tìm được một vị
trí xác định của các engram ). Song một điều ngạc nhiên là dù cắt bỏ bao nhiêu
đi nữa kỹ năng được huấn luyện vẫn lưu tồn. Và Pribram đi đến kết luận quan
trọng: trí nhớ không được lưu trữ tại một nơi nào cả trong não bộ mà bằng
một cách nào đó lan truyền và phân bố trong toàn não bộ [5b] và ông hiểu
rằng: não bộ là một toàn ảnh (hologram).
Trí nhớ được xem như là
những xung lượng thần kinh đan chéo chằng chịt trong não bộ tương tự như những
hình ảnh giao thoa tia laser trên một diện tích của hologram.
Nếu như một phần của hologram có khả
năng tái tạo toàn ảnh của một vật thì mỗi phần của não bộ cũng chứa tất cả
thông tin để phục hồi toàn bộ trí nhớ.
Bohm và Pribram gặp nhau
Các lý thuyết của Bohm và Pribram đã
tạo nên một quan điểm sâu sắc về nhận thức luận đối với thế giới khách quan: toàn
bộ vũ trụ là một toàn ảnh (the entire universe is a hologram), bộ não là
một hologram cuộn vào trong vũ trụ toàn ảnh (the brain is a hologram enfolded
in a holographic universe).
Năm 1982 Alain Aspect (Đại học
Paris) đã thực hiện một thí nghiệm có thể nói là quan trọng nhất trong thế kỷ
20, liên quan đến nghịch lý EPR , chứng minh rằng trong những điều kiện nhất
định các hạt như electron có thể tức thời
liên lạc với nhau (vậy vận tốc truyền thông tin lớn hơn vận tốc ánh
sáng) bất kể khoảng cách giữa chúng là 10 m hay 10 triệu dặm , đó là hiện tượng
liên đới lượng tử – quantum entanglement .
Theo David Bohm thì thí nghiệm của
Aspect càng chứng minh vũ trụ quả là một hologram. Trong nghịch lý EPR , theo
Bohm thì Einstein sai lầm vì cho rằng hệ đó là hai hạt riêng lẻ trong khi phải
xét chúng như một hệ không phân chia được.
Và không phải các electron đã truyền
thông tin cho nhau theo một cách bí ẩn nào đó mà là sự phân cách giữa chúng chỉ
là một ảo tưởng. Tại một mức sâu các hạt đó không là những thực thể riêng lẻ mà
chỉ là những biểu kiến của một thực thể cơ bản.
Rộng hơn mọi thành phần của vũ trụ ở
một mức sâu đều liên thông với nhau (interconnectedness) và ngược lại vũ trụ
hiện hữu trong mỗi bộ phận ("whole in every part"). Theo Bohm ta
thấy được những thực thể riêng biệt chỉ vì ta chỉ nhìn được một khía cạnh của thực
tại. Các thực thể riêng biệt đó chỉ là những bóng ma (eidolon) còn vũ trụ tự
thân là một hình chiếu, nói cách khác là một hologram.
Các electron của nguyên tử carbon
trong não bộ của con người liên thông với các nguyên tử của mỗi con cá hồi đang
bơi, của mỗi quả tim đang đập và của những vì sao đang chiếu sáng trên bầu
trời.
Vì sự liên thông phổ quát này mà
trong vũ trụ toàn ảnh , thậm chí không gian và thời gian không còn là
cơ bản nữa!
Những khái niệm như tọa độ và thời
điểm sẽ không còn ý nghĩa trong một vũ
trụ mà không vật gì được tách rời với vật khác trong không gian và thời gian, ý
thức không tách rời với vật chất (đây là cách tiếp cận vấn đề ý thức của Bohm
). Tại mức sâu hơn này, thực tại là một siêu hologram trong đó quá khứ,
hiện tại và tương lai quyện vào nhau và tồn tại đồng thời . Tại mức sâu siêu hologram nếu tìm được phương pháp thích hợp chúng ta
có thể làm tái hiện được những cảnh tượng từ quá khứ xa xôi.
Sự tổng hợp hệ thống ý tưởng của Bohm và Bribram dẫn đến là hệ mẫu toàn ảnh HP
(Holographic Paradigm ). Nhiều nhà khoa học công nhận rằng nhiều hiện tượng
ngoại tâm lý học (para-psychological) như thần giao cách cảm , luân hồi . tiên tri... có thể hiểu được nhờ
HP.
Thời gian sẽ trả lời HP đúng hay sai
song hiện tại HP ,vì hàm lượng triết lý lớn,
đang làm say đắm nhiều nhà khoa
học và là nguồn cảm hứng dồi dào cho điện ảnh (các phim
'The Matrix', 'The 13th Floor', Star
Trek...) cho nghệ thuật, văn chương.
Một kiểm chứng
thực nghiệm : phát hiện tiếng ồn toàn ảnh (holographic
noise) của dự án GEO600?
GEO600 là một
dự án hợp tác giữa Viện Vật lý hấp dẫn Max Planck, Đại học Leibniz Hannover, Đại học
Cardiff, Đại học Glashow và Đại học Birmingham. GEO600 là một detector dài 600 m, xây dựng tại Hannover (Đức) có mục tiêu
tìm sóng hấp dẫn phát ra từ những thiên thể như sao neutron, lỗ đen.
Hiện nay
GEO600 chưa tìm ra sóng hấp dẫn song rất
có thể đã phát hiện một hiện tượng quan trọng nhất trong thế kỷ này. Trong
nhiều tháng qua đội ngũ GEO600 đau đầu vì một nhiễu loạn, một tiếng ồn không
giải thích được trong detector của họ.
Một
điều đáng ngạc nhiên, Craig Hogan , Giám đốc Trung tâm Vật lý thiên văn các hạt
cơ bản, Phòng thí nghiệm Gia tốc quốc gia Fermi , GS Đại học Chicago, Illinois
lại tiên đoán được rằng nhóm GEO600 chắc sẽ gặp vấn đề về tiếng ồn lạ lùng này
và đưa ra cách giải thích: nhóm GEO600 đã tiến đến giới hạn cơ bản của không
thời gian, đã tiến đến điểm mà continium
phẳng phiu của Einstein chấm dứt nhường chỗ cho cấu trúc dạng “hạt” gián đoạn,
nhóm GEO600 đã chạm ngõ đến sự thăng giáng “run rẩy” lượng tử của không thời
gian, một mức sâu của thực tại trong vũ trụ hologram . Tại những khoảng cách vi
mô với kích thước cỡ 10 – 35 m ( độ dài Planck) không thời gian có
cấu trúc gián đoạn như cấu tạo được bằng những pixel .
GS
Bernard Schutz (Viện Thiên văn Hoàng gia Anh) viết: nếu tiếng ồn toàn ảnh được
phát hiện thì đây là tín hiệu của một kỷ
nguyên mới trong vật lý cơ bản [5c]. Gs Karsten Danzmann, Giám đốc Viện Albert Einstein
Hannover dè dặt hơn phát biểu: vấn đề tiếng ồn toàn ảnh đã đặt nhóm nghiên cứu
GEO600 vào tâm cơn lốc của một nghiên cứu cơ bản quan trọng của thế kỷ. Nhóm
các nhà vật lý GEO600 đang tích cực thu thập dữ liệu để chứng minh liệu
tiếng ồn họ thu được có phải là tiếng ồn toàn ảnh hay không?
Nếu
nhóm GEO600 đã tìm thấy những gì mà Craig Hogan phỏng đoán thì chúng ta đang
ở trong một hologram vũ trụ khổng lồ ( Our World May Be a Giant Hologram ).
Trong vũ trụ
toàn ảnh mọi thực thể trong không gian
và thời gian đều liên thông với nhau (interconnectedness) và cách tiếp cận toàn
ảnh giúp thống nhất hấp dẫn và lượng tử ( bài toán số một của vật
lý ) và rộng hơn cung cấp một tầm nhìn
nhất quán đối với mọi hiện tượng thuộc vật lý, sinh học, bệnh học, tâm lý học,
ngoại tâm lý học (parapsychology)...
Vũ trụ toàn ảnh nếu đúng sẽ mở ra một kỷ
nguyên khoa học mới có chiều sâu hơn hiện nay,
có tầm bao quát một cách thống nhất nhiều hiên tượng (từ vật lý đến các
khả năng kỳ diệu của não bộ) mà khoa học hiện nay chưa có lời giải thích . Vũ trụ toàn ảnh sẽ có tác động lớn đến triết học và là nguồn
cảm hứng của nhiều ngành nghệ thuật. Nhiều nhà khoa học xếp lý thuyết Vũ trụ
toàn ảnh ở tuyến đầu
tri thức (latest frontier of
knowledge), lý thuyết Vũ trụ toàn ảnh có nội dung lớn hàm ẩn cả toán, lý, sinh,
triết học...
6 . Kết luận
Dưòng như việc
nghiên cứu tách rời hai vương quốc sống và không sống chỉ là một biểu hiện của
sự hạn chế nhận thức của chúng ta trong
một giai đoạn của lịch sử khoa học. Tuy rằng hiện nay chúng ta chưa đủ khả năng
để hiểu hết bí mật lớn của sự sống song những cơ sở ban đầu dựa trên lý thuyết
động học vi mô (kinetics theory), lý thuyết phức hợp ( complexity theory ), lý
thuyết tai biến (catastrophe theory), lý thuyết lượng tử để nghiên cứu các cấu
trúc phát tán (dissipative), các quá trình tự tổ chức (self-organization) cũng
cho phép chúng ta có được những tiếp cận ban đầu từ nhiều phía hoặc định tính
hoặc ít nhiều định lượng đến bí mật lớn này.
Hơn nữa như chúng ta thấy theo quan điểm vũ trụ toàn
ảnh của Bohm và Pribram thì hai vương quốc của vật chất sống và không sống liên
thông với nhau.
Tất cả những
điều nói trên cho phép chúng ta kết luận rằng giữa hai vương quốc của vật chất
sống và không sống dường như không tồn tại một ma lực nào ngoại trừ những đột
sinh (emergences) mà chúng ta chưa tìm ra được các quy luật hình thành.
Tài liệu tham
khảo
[1a] Y.Korchounov,Fondements mathématiques de
la cybernétique
[1b] Hermann Haken, Synergetics, An
ỉntroduction, Nonequilibrium Phase Transitions and Self-Organization in
Physics, Chemistry and Biology
*
[2a] Von Dr. Werner Ebeling, Eine Einfuhring
in die Theorie dissipativer Strukturen
[2b] Iu.B.Rumer & M.Ch.Rybkin, Thermodynamics,
Statistic Physics and Kinetics
[2c] E.M.Lifchitz, L.P.Pitaevski , Physical
kinetics
*
[3a] Edgar Morin , Introduction à la pensée
complexe, Nhập môn tư duy phức hợp
Nhà xuất bản
tri thức
[3b] Heinz R. Pagels (1988), The
Dreams of Reason: The Computer and the Rise of the Sciences of Complexity(1988)
[3c] Michel Bitbol, Robert Laughlin, Cécile
Michaut, La Recherche số 405, tháng hai/2007
[3d] René Thom,
Structural Stability and Morphogenesis (Ổn định cấu trúc và sự tạo
sinh các hình thái),
Benjamin-Cummings Publishing, Reading, Massachusetts, 1975.
[3e] J.M.T.Thompson, Instabilities and
Catastrophes in Science & Engineering 1982
*
[4a] Jerzy Jurkiewicz,
Renate Loll and Jan Ambjorn,The Self- organizing Quantum Universe), Scientìific
American, tháng 07/ 2008
[4b] Leonard Susskind, Physicsworld, July
2009
[4c] Raphael Bousso, Joseph Polchinski,
The string theory landscape, Scientific American, tháng 9/2004
*
[5a] David Bohm, Wholeness and the implicate
Order, 1980.
[5b] Michael Talbot, The holographic
Universe,1996.
[5c] Bernard Schutz, ScienceDaily, Feb.4/2009.
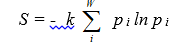















Nhận xét
Đăng nhận xét